【数学】人類史を変えた世界最高峰の数学者15人

数学は、しばしば「最も純粋な知の探究」と呼ばれます。

数式の背後には、美しさと論理が織りなす壮大な世界が広がり、人類の歴史を通じて数多くの天才たちがその扉を開いてきました。

彼らの発見は、科学や技術の発展を支えただけでなく、私たちの世界の見え方そのものを変えてきたと言っても過言ではありません。

本記事では、そんな数学史に名を刻んだ「世界の優れた数学者トップ15」を厳選して紹介します。

それぞれの人物がどのような問題に挑み、どんな革新的な成果を残したのか。その足跡をたどることで、数学という学問の奥深さと魅力がより鮮明に見えてくるはずです。

1. カール・フリードリヒ・ガウス（1777–1855）

カール・フリードリヒ・ガウスは、「数学の王」と称され、古今東西の数学者の中でも突出した才能を持つ人物として語られ続けています。

1777年にドイツの貧しい家庭に生まれましたが、その才能は幼少期から異常なほど際立っていました。

幼い頃、教師が「1から100までの合計を求めよ」という課題を出した際、ガウスは数秒で答えを導き出した逸話が有名です。

普通に考えれば、1+2+3+4+5・・・・などと計算していく為、回答を出すには多少の時間がかかります。

しかし、天才であるガウス少年にはより速い計算方法が瞬時に閃いたのでした。

規則性を直感的につかみ、等差数列の公式を即座に見抜いたというエピソードは、後世まで語り継がれる象徴的な瞬間となっています。

その後、貴族の支援を受けて大学に進み、学生時代から既に数論、代数学、解析学、天文学など多彩な分野で成果を重ねました。

特に背景にほとんどヒントがなかったにもかかわらず、17歳のときに正17角形がコンパスと定規だけで作図できることを発見した功績は、数学史上における圧倒的な快挙です。

この発見を皮切りに、彼の才能はさらに開花していき、以後の業績はどれも「一分野を丸ごと変えてしまうレベル」と称されるほどでした。

ガウスの代表的な成果としては、現代の数学に直結するものがいくつもあります。
代表例としては、

• 数論の基礎を築いた『算術研究』
• 統計学の中心概念「正規分布（ガウス分布）」の確立
• 最小二乗法の発明によるデータ解析手法の確立
• ガウスの法則など物理学への巨大な影響

が挙げられ、どれも後世の科学全般に決定的な影響を残しています。

また、ガウスは慎重で完璧主義者として知られ、証明にわずかな不備でもあると公表を控える傾向がありました。

実際、非ユークリッド幾何学に関する着想を誰よりも先に持っていたにもかかわらず、「世間が理解できないだろう」という理由から発表しなかったとされています。

この寡黙さが逆に伝説性を高め、「彼が生涯で公表しなかった発見はどれほどあったのか」という議論も現在まで続いています。

晩年まで精力的に研究を続けたガウスは、多分野にわたる業績によって、現代数学の骨格をつくりあげた人物とも言える存在です。

どの角度から見ても、数学史において頂点級の天才であり、「ガウスの名前を知らずに科学を語ることはできない」と評されるほど圧倒的な影響力を持つ数学者として記憶されています。

ガウスの天才エピソード

● 子どもの頃から“計算が速すぎた”問題児

小学校で、教師が「1から100までの和を求めよ」という時間つぶし課題を出したとき、ガウスは数秒で答えを出し、教師を驚愕させました。
これはよく知られた話ですが、実は教師は“生徒が静かになるまでの時間稼ぎ”のつもりだったという説もあり、ガウスだけが即座に終わらせてしまったため、逆に教師が困ったというオチ付きです。

● 結婚式の日でさえ計算を止めない

結婚式の直前、ガウスは計算に没頭していて、周囲が何度呼んでも気づかなかったと伝えられています。
ようやく呼び出されても「あとちょっとで結論が出るのに…」と不満げだったという逸話が残っています。

● 子どもの名前すら研究の邪魔に？

ガウスは研究に集中しすぎて家庭のことをよく忘れ、子どもの名前を思い出せないことがあったと言われています。
一方で数学の問題は数十年前の未完成メモを即座に理解して続きを解いた、という恐るべき頭脳の持ち主でした。

📖関連書籍

2. アーキメデス（紀元前287–212）

アーキメデスは、古代ギリシャが生んだ最大級の数学者として知られ、その業績は2000年以上経った現代においても色あせることがありません。

紀元前287年、シチリア島シラクサの裕福な家庭に生まれ、幼い頃から数学・機械工学・天文学に強い興味を示していたと伝えられています。

王族とも親交があり、宮廷に出入りしながら研究を進める恵まれた環境にあった一方、その探究心は常軌を逸するほど強く、数学に没頭して周囲の声が耳に入らなかったという逸話も残っています。

アーキメデスの名が歴史の中で語り継がれている最大の理由は、当時としては異例の「厳密な数学的思考」を徹底していた点にあります。

円周率の計算を飛躍的に精密化したり、微積分の概念につながる“無限小”の考え方を先取りしていたりと、彼の手法は明らかに時代を1000年以上先取りしていました。

また、有名な“浮力の原理”の発見では、浴槽から立ち上がって「見つけたぞ！」と叫びながら街中を走り回ったというエピソードが語られるほど、強烈な好奇心と発想力を持っていた人物です。

アーキメデスの代表的な成果としては、後世の数学と物理学に直接影響を与えたものがいくつもあります。
例としては、

• 円や球、放物線の面積・体積に関する高度な理論を構築したこと
• てこの原理を数学的に説明し、力学の基礎を確立したこと
• 浮力の法則（アーキメデスの原理）を発見したこと
• 戦争時に用いられた投石機や反射鏡兵器など、工学的技術を発明したこと

などが挙げられ、どれも後の科学発展に欠かせない土台を形成しました。

さらに、アーキメデスは生涯を通じて研究に没頭し、外敵の侵入が迫る戦時下でも図形を描き続けていたと伝えられています。

彼は敵兵に斬られて生涯を閉じますが、その最期の言葉とされる「私の円を乱すな」は、彼の数学への情熱を象徴する名言として知られています。

この徹底した研究者気質は、歴史に残る天才のイメージをより強烈にしています。

アーキメデスの残した業績は、数学・物理・工学すべてに深く根を張り、まさに古代における“総合科学者”であったと言える存在です。

その影響力はガウスやニュートンと並び称されるほど大きく、「アーキメデスなくして科学の歴史は語れない」と評されるほど、圧倒的な存在感を持ち続けています。

アーキメデスの天才エピソード

● お風呂に入って「エウレカ！」と叫びながら街を走る

アーキメデスが浮力の原理を発見した場面はあまりにも有名です。
彼は浴槽の水位が上がる様子を見て仕組みを理解し、その瞬間に興奮のあまり「見つけたぞ！」（ギリシャ語で Eureka!）と叫び、裸のまま街中を走り回ったと伝えられています。
現代なら完全にアウトですが、それほど発見が嬉しかったということです。

● 戦争中でも数式のほうが大事だった

ローマ軍がシラクサに侵攻した際、アーキメデスは砂の上に図形を描きながら問題を考えており、兵士に声をかけられても振り向きませんでした。
兵士が怒って彼を斬ってしまった際の最期の言葉とされるのが「私の円を乱すな」です。
命より数学優先、という究極の天才らしい最期です。

● 科学者なのに“兵器の発明”も天才的

投石機、滑車装置、鏡で太陽光を反射して船を燃やす“熱光線装置”など、彼は戦争のための発明も多数生み出しました。
ただし、本人は「本当は純粋数学の方が好きだった」と言っていたそうです。

📖関連書籍

3. アイザック・ニュートン（1642–1727）

アイザック・ニュートンは、科学史において最も影響力の大きい人物の一人であり、数学・物理学・天文学といった幅広い領域で革命的な成果を残しました。

1642年、イングランドの地方に生まれ、幼少期は病弱で控えめな少年だったといわれています。

しかし、ひとたび学問と向き合うと驚異的な集中力を発揮し、ケンブリッジ大学に入学してからは持ち前の洞察力が一気に開花しました。

1665年、ペストの流行による大学閉鎖で故郷に戻っていたわずか数年の間に、微積分法、光の理論、万有引力のアイデアをほぼすべて思いついていたという逸話は、ニュートンの天才性を象徴するものです。

特に数学分野では、ライプニッツとは独立に微積分を創始し、後世の科学を根底から支える計算基盤を作り上げました。

彼が用いた「流率法」は現代の微積分とは形式が異なるものの、変化を数量化するという核心部分は現在の理論にも直結しています。

また、プリンキピアで示した運動の三法則と万有引力の法則は、天体の動きを“数式で説明できる”ことを示し、人類の世界観を根本から変える結果となりました。

ニュートンの代表的な功績としては、後の科学革命を決定づけるほどの影響力を持つものがいくつもあります。

• 微積分法（流率法）の創始
• 光学の研究における“光の分解”と“色の理論”の確立
• 運動の三法則と万有引力の法則による古典力学の確立
• 反射望遠鏡（ニュートン式望遠鏡）の発明

などが挙げられ、どれもが科学の枠組みそのものを作り替えた成果ばかりです。

また、ニュートンは極端なまでの完璧主義者であり、批判を恐れて研究成果の発表に慎重だったことでも知られています。

ライプニッツとの微積分論争に見られるように気難しい一面もありますが、その根底には「誤りを出してはならない」というストイックな姿勢がありました。

生涯の後半には王立協会の会長となり、当時の科学界を牽引する立場となりますが、その一方で錬金術や神学の研究に没頭していたという側面もあり、謎めいた人物像としても語られています。

晩年まで知的探究心を失うことなく生きたニュートンは、まさに“科学革命を具現化した人物”と言える存在です。

現代科学のほぼすべてがニュートン力学を基盤として発展したことを考えれば、「ニュートンなしに自然科学は成立しない」と言われるのも決して誇張ではありません。

彼の名は、今なおガウスやアーキメデスと並んで、世界最高峰の天才として語り継がれています。

アイザック・ニュートンの天才エピード

● リンゴは落ちるがニュートンは落ち着かない

古典的な“リンゴの話”は脚色も多いですが、実際にニュートンは木からリンゴが落ちるのを見たとき、「なぜ真下に落ちるのか」と本気で考え始め、そこから万有引力のヒントを掴んだとされています。
普通の人は「落ちたな」で終わるのに、ニュートンは宇宙の法則を考え始めるのですから、桁違いです。

● 研究に没頭しすぎて料理を燃やす

ニュートンは、食事の準備をしている最中に数式を考え始め、鍋を火にかけたことすら忘れたと言われています。
気づいた時には料理は炭の塊。
「なぜこんな匂いが？」と思ったら自分の家から煙が出ていたという笑えない話が残っています。

● 研究ノートを“秘密語”で書いていた

ニュートンは極度に慎重で、自分の研究が理解されないことを恐れ、ノートを暗号のような書き方で残していました。
後世の学者が解読するのに非常に苦労したと言われており、「天才の頭の中を見ようとするのは危険」という教訓になっています。

📖関連書籍

4. レオンハルト・オイラー（1707–1783）

レオンハルト・オイラーは、18世紀を代表する数学者であり、現代数学の基礎を事実上つくり上げた人物として知られています。

1707年にスイスで生まれ、幼少期から数学に強い才能を示しましたが、当初は神学者になる道も考えられていました。

しかし、その非凡な計算能力と抽象的思考力は周囲の学者の目に留まり、若くして数学の道へと進むことになります。

オイラーの最大の特徴は、その業績の量と幅の異常さにあります。

解析学、数論、幾何学、力学、天文学、流体力学など、ほぼあらゆる分野に決定的な貢献を残しました。

現在当たり前のように使われている数学記号や表記法の多くも、オイラーによって定着したものです。

関数を f(x) と表す記法や、自然対数の底 e、虚数単位 i などは、彼の仕事なしには存在しなかった可能性すらあります。

オイラーの代表的な功績としては、数学の言語そのものを整備した点が特に重要です。
例としては、

• 解析学を体系化し、微積分を実用的な学問へと押し上げたこと
• 自然対数の底 e の研究と指数関数の理論確立
• 複素数を本格的に数学へ組み込んだこと
• オイラーの公式 e^{iπ} + 1 = 0 による数学的美の象徴的表現

などが挙げられ、どれも現代数学の根幹を成す成果です。

さらに驚くべきことに、オイラーは晩年にほぼ失明した状態でも研究を続け、口述筆記によって膨大な論文を生み出し続けました。

その生涯で残した論文・著作は800本以上にのぼり、「一人で一時代分の数学を書いた」と評されるほどです。

オイラーは、天才という言葉を“量と質の両面”で体現した、極めて稀有な数学者として記憶されています。

レオンハルト・オイラーの天才エピソード

● 目が見えなくなっても計算精度は変わらない
オイラーは晩年にほぼ完全に失明しましたが、それでも複雑な計算や証明を頭の中で行い、弟子に口述する形で論文を書き続けました。
周囲が心配すると、「計算するには目は必要ない」と言ったと伝えられています。

● 記号を“発明”してしまう癖
考えを整理するために新しい記号を次々と導入し、それがそのまま世界標準になりました。
結果として、現代人はオイラーの思考様式で数学を学ばされている、とも言われています。

● 家庭的で穏やかな天才
天才にありがちな奇人変人タイプではなく、13人の子どもを持つ家庭人で、性格も温厚でした。
「天才＝変人」というイメージを良い意味で裏切る存在です。

📖関連諸説

5. ドン・パルメニデス／ユークリッド（紀元前300年ごろ）

ユークリッドは、古代ギリシャを代表する数学者であり、「幾何学の父」として知られる人物です。

生没年や私生活についてはほとんど記録が残っていませんが、紀元前300年頃、エジプトのアレクサンドリアで活動していたと考えられています。

彼の名を不朽のものにしたのは、数学史上最も影響力のある書物の一つである『原論』です。

『原論』は、幾何学を中心に数学を公理・定義・定理という論理構造で体系化した書物であり、その完成度は驚異的でした。

ユークリッドは、直感や図形的感覚に頼るのではなく、「最小限の前提から論理的にすべてを導く」という方法を確立し、数学を“厳密な学問”へと引き上げました。

この形式は、数学だけでなく、哲学や科学の思考法にも深い影響を与えています。

ユークリッドの功績は、個々の発見というよりも、数学の書き方そのものを定義した点にあります。
代表的な意義としては、

• 幾何学を公理体系として完成させたこと
• 論理的証明というスタイルを標準化したこと
• 2000年以上にわたり教科書として使われ続けた『原論』の編纂

などが挙げられます。ニュートンやガウスを含む、ほぼすべての数学者が、何らかの形でユークリッドの方法論を学んでいます。

ユークリッドは派手な逸話の少ない人物ですが、その静かな影響力は計り知れません。

「ユークリッド以前」と「ユークリッド以後」で数学の姿が明確に分かれると言われるほど、学問の基礎構造を作り上げた存在です。

ユークリッドの面白エピソード

● 「数学に王道なし」
ある王が「幾何学を簡単に学ぶ方法はないのか」と尋ねた際、ユークリッドは
「幾何学に王道はありません」
と答えたと伝えられています。
身分や地位に関係なく、努力なしでは理解できないという、あまりにも冷静な名言です。

● 徹底的に無駄を削ぎ落とす性格
『原論』では、余計な説明や装飾的表現がほぼ存在せず、淡々と論理だけが積み重ねられています。
この無機質さが、逆に2000年以上使われ続ける理由になりました。

● 個人の功績より体系を重視
ユークリッド自身のオリジナル発見は意外と少ないとも言われますが、それを補って余りある「まとめる力」がありました。
天才は必ずしも“発見者”である必要はない、という好例です。

📖関連書籍

6. ヘンリク・ポアンカレ（1854–1912）

アンリ・ポアンカレは、19世紀末から20世紀初頭にかけて活躍したフランスの数学者であり、「最後の万能数学者」とも呼ばれる存在です。

1854年にフランスで生まれ、幼少期から並外れた記憶力と空間把握能力を示していました。

一方で、計算はやや苦手だったとも言われており、後年の彼の数学が「計算よりも構造と直観を重視する」方向へ進んだ理由の一つと考えられています。

ポアンカレの最大の特徴は、数学・物理・哲学を横断する圧倒的な洞察力にあります。

トポロジーの創始、力学系の研究、カオス理論の原型、相対性理論の先駆的アイデアなど、その業績はあまりにも多岐にわたります。

特に、三体問題の研究から生まれた“非線形系の複雑な振る舞い”の理解は、「決定論的な世界でも予測不能な現象が生じる」ことを数学的に示し、後の科学観に大きな転換をもたらしました。

ポアンカレの代表的な功績としては、現代科学に直結する本質的なものが並びます。
例としては、

• トポロジーという新しい数学分野の創始
• 三体問題の研究を通じたカオス理論の萌芽
• 相対性理論に先行する時間・空間の考察
• 「ポアンカレ予想」による幾何学・トポロジーへの深遠な問い

などが挙げられ、どれも20世紀科学の方向性を先取りした成果です。

また、ポアンカレは数学的発見のプロセスそのものについても深い洞察を残しており、著書『科学と方法』では「無意識の思考が創造性を生む」という独自の理論を展開しています。

彼は単なる計算の名人ではなく、「なぜ数学が成立するのか」を考え続けた哲学的天才でした。

理論の深さと視野の広さという点で、ポアンカレは他に類を見ない存在として語り継がれています。

ポアンカレの面白エピソード

● 発見は“机の前”ではなく“乗合馬車のステップ”で起きた
ポアンカレは、長く悩んでいた数学的問題の解決策を、休暇中に乗合馬車に乗り込む瞬間、突然ひらめいたと語っています。
考えるのをやめた瞬間に答えが現れた、という体験は創造性研究の定番例です。

● 計算が苦手な数学者
暗算や長い計算は得意ではなく、学生時代の試験では計算ミスをすることもありました。
それでも本質を一瞬で見抜く力は群を抜いており、「構造を見る天才」と評されました。

● 講義が速すぎて誰もついていけない
黒板に向かって猛烈なスピードで書き続けるため、学生はノートを取ることすらできなかったそうです。
天才の思考速度がそのまま授業に反映されていました。

📖関連書籍

7. デイヴィッド・ヒルベルト（1862–1943）

ダフィット・ヒルベルトは、20世紀数学の方向性を決定づけたドイツの数学者であり、「近代数学の設計者」とも呼ばれる存在です。

1862年にドイツで生まれ、若い頃から抽象的な思考に優れ、代数学・幾何学・解析学など幅広い分野で成果を上げました。

特に、個々の問題を解くだけでなく、「数学全体をどう構築すべきか」を考え続けた点に、ヒルベルトの本質があります。

ヒルベルトは、1900年の国際数学者会議で発表した「ヒルベルトの23の問題」によって、20世紀数学の研究課題を事実上提示しました。

このリストは単なる問題集ではなく、「これからの数学は何を目指すべきか」という指針そのものであり、以後100年以上にわたって数学研究の道標となっています。

彼の影響力は、直接の研究成果以上に、この“方向づけ”の力にあります。

ヒルベルトの代表的な功績としては、数学の基礎構造に関わるものが中心です。
例としては、

• ヒルベルトの23の問題による研究指針の提示
• 幾何学の公理化による論理的再構築
• 関数解析の基礎確立（ヒルベルト空間）
• 数学の完全性・無矛盾性を目指すヒルベルト・プログラム

などが挙げられ、現代数学の土台を形成しています。

ヒルベルトは、明快で前向きな科学観を持つ人物でもあり、「我々は知ることができるし、知るであろう」という有名な言葉に象徴されるように、人間の理性に強い信頼を寄せていました。

その楽観主義は、後にゲーデルの不完全性定理によって一部否定されることになりますが、それでもヒルベルトの挑戦が数学を飛躍的に前進させた事実は変わりません。

ヒルベルトの面白エピソード

● 数学界に“宿題”を出した男
ヒルベルトは23の問題を提示することで、世界中の数学者に一斉に宿題を出しました。
結果として、20世紀数学の大半はこの宿題を解く過程で発展したと言われています。

● 楽観主義がすごすぎる
数学は必ず完全に理解できると信じ、「解けない問題は存在しない」と本気で考えていました。
この姿勢が多くの若い数学者を勇気づけました。

● ゲーデルの登場にも動じない
不完全性定理によって自身の構想が打撃を受けた後も、ヒルベルトは
「それでも数学は前進する」
という姿勢を崩さなかったと伝えられています。

📖関連書籍

8. アンドリュー・ワイルズ（1953–）

写真出典：著作権 CJ Mozzochi、プリンストン NJ」, Attribution, via Wikimedia Commons

アンドリュー・ワイルズは、20世紀後半から21世紀にかけて活躍したイギリスの数学者であり、「フェルマーの最終定理を証明した男」として世界的に知られています。

1953年にイングランドで生まれ、10歳のときに図書館でフェルマーの最終定理の存在を知ったことが、彼の人生を決定づけました。

「この問題を自分が解きたい」と強く思ったその瞬間から、ワイルズの数学者としての物語は始まったと言われています。

長い年月を経て研究者となったワイルズは、1990年代初頭、誰にも告げずにフェルマーの最終定理の証明に取り組み始めました。

この定理は300年以上にわたり証明されておらず、もはや“象徴的存在”と化していた問題です。

ワイルズは当時最先端だった楕円曲線とモジュラー形式を結びつける理論を駆使し、7年間にわたる極秘研究の末、ついに証明にたどり着きました。

ワイルズの功績は、単に難問を解いたという点にとどまりません。彼の証明は、数学の複数分野を深く結びつけ、数論の地形そのものを大きく塗り替えるものでした。

代表的な意義としては、

• フェルマーの最終定理の完全証明
• 谷山–志村予想（モジュラー性定理）の大幅な進展
• 数論と幾何学の強力な統合

などが挙げられ、現代数学における最重要成果の一つと評価されています。

一度は証明に欠陥が見つかるという劇的な展開もありましたが、ワイルズは決して諦めず、元教え子とともに問題を克服しました。

この粘り強さと純粋な情熱は、「努力と執念が天才を完成させる」ことを体現した例として、多くの人に感動を与えています。

ワイルズの面白エピソード

● 7年間、誰にも話さなかった秘密研究
ワイルズは、同僚や家族にすら研究内容を明かさず、完全に一人で証明に取り組んでいました。
学会にもほとんど顔を出さず、「姿を消した数学者」と噂されていたほどです。

● 発表直前の大どんでん返し
歴史的発表の後、致命的な欠陥が発覚しましたが、絶望的な状況から一年かけて修正に成功しました。
この展開は「数学史上最もドラマチックな証明」と呼ばれています。

● 少年時代の夢を一生かけて回収
10歳で憧れた問題を、大人になって本当に解いてしまった例は極めて稀です。
ワイルズは「数学者は夢を見続けていい」という象徴的存在となりました。

9. アレクサンドル・グロタンディーク（1928–2014）

写真出典：Konrad Jacobs, Erlangen, Copyright by MFO / Original uploader was AEDP at it.wikipedia – https://opc.mfo.de/detail?photoID=1452 / Transferred from it.wikipedia, CC BY-SA 2.0 de, https://commons.wikimedia.org/w/index.php?curid=3906524による

アレクサンドル・グロタンディークは、20世紀数学において最も革命的な影響を与えた人物の一人であり、特に代数幾何学の分野を根底から作り替えた数学者です。

1928年にドイツで生まれ、波乱に満ちた幼少期を送りましたが、その過酷な環境とは対照的に、数学的才能は異様なほど純粋で圧倒的でした。

グロタンディークの本質は、個々の問題を解くことよりも、「数学の見方そのものを変える」点にあります。

彼は既存の理論を細部から修正するのではなく、より高い抽象度の枠組みを導入し、問題が自然に解けてしまう構造を作り出しました。

スキーム、層、トポスといった概念は、その象徴的な成果です。

グロタンディークの代表的な功績としては、現代数学の基盤を再設計した点が挙げられます。
例としては、

• 代数幾何学の全面的再構築（スキーム理論）
• 層とコホモロジー理論の飛躍的発展
• ヴェイユ予想解決への決定的貢献（間接的影響）
• 抽象化を極限まで押し進めた新しい数学的言語の創造

などがあり、その影響は現在も研究の最前線に及んでいます。

しかし、グロタンディークは名声や権威から距離を置く人物でもありました。

数学界の中心で圧倒的な成果を出した後、突如として第一線から姿を消し、社会や文明そのものに批判的な立場を取るようになります。

その生き方は、天才のもう一つの極端な形として語られています。

グロタンディークの面白エピソード

● 定義から全部作り直す
問題を解く前に「そもそも定義が悪い」と言い、理論全体を再構築してしまいました。
周囲は理解不能でも、後から見るとすべてが合理的だったという例が多々あります。

● フィールズ賞を事実上“拒否”
数学界最高の栄誉であるフィールズ賞を受賞しましたが、名誉や競争に興味を示さず、淡々としていました。
評価されること自体に価値を見出さなかった天才です。

● 突然の隠遁生活
50代で数学界から完全に姿を消し、山中で隠遁生活を送りました。
「世界よりも真理の方が重要だった」と言われる生き方です。

📖関連書籍

10. ソフィー・ジェルマン（1776–1831）

ソフィー・ジェルマンは、18〜19世紀にかけて活躍したフランスの数学者であり、女性が正式に数学教育を受けることがほぼ不可能だった時代に、独学で最先端の数学へ到達した先駆者です。

1776年にパリで生まれ、フランス革命という激動の時代を生きながら、数論と数学物理の両分野で重要な業績を残しました。

ジェルマンの本質は、才能そのもの以上に、学ぶことを許されない環境でも思考を止めなかった精神の強さにあります。

彼女はエコール・ポリテクニークの講義録を密かに入手し、男性名義でレポートを提出するなど、あらゆる制約を迂回しながら数学に食らいつきました。

その過程で生まれた研究は、後世の数学に確かな足跡を残しています。

ソフィー・ジェルマンの代表的な功績としては、以下のような点が挙げられます。

• フェルマーの最終定理に関する部分的成果（ソフィー・ジェルマンの定理）
• 弾性理論・振動理論における数学的基礎の構築
• 数論と物理学を横断する独自の視点の確立
• 女性数学者の道を切り拓いた象徴的存在

これらの成果は、当時の評価を大きく超えて、現在になってその重要性が再認識されています。

彼女の人生は、正当な評価や地位からは程遠いものでしたが、それでもジェルマンは数学を手放しませんでした。

理解されなくても、認められなくても、思考すること自体が価値である。その姿勢は、数学史において特別な輝きを放っています。

■ ソフィー・ジェルマンの面白い天才エピソード

● 男性名義で数学界に潜入
女性であることを理由に排除されるのを避け、「M.ル・ブラン」という男性名を使って研究を発表していました。
後にガウスが正体を知り、その才能を心から称賛したと伝えられています。

● フェルマーの最終定理に真っ向挑戦
当時ほとんど誰も太刀打ちできなかった難問に、独力で理論的突破口を与えました。
この成果は、後世の研究の重要な礎となります。

● 評価されなくても折れない
公式な職も地位も与えられませんでしたが、数学への情熱が衰えることはありませんでした。
静かで、しかし揺るぎない天才です。

11. エヴァリスト・ガロア（1811–1832）

エヴァリスト・ガロアは、19世紀フランスに現れた数学史上屈指の早熟かつ悲劇的な天才であり、わずか20歳で生涯を終えながら、現代数学の根幹を築いた人物です。

1811年に生まれ、短くも激烈な人生の中で、代数学の構造を根本から変える発想に到達しました。

ガロアの本質は、方程式を「解く」ことではなく、なぜ解けるのか、なぜ解けないのかを構造として理解した点にあります。

彼は計算の技巧ではなく、対称性という抽象概念に注目し、後に「ガロア理論」と呼ばれる革命的枠組みを生み出しました。

ガロアの代表的な功績としては、以下が挙げられます。

• 代数方程式の可解性を群論で説明する理論の創始
• 現代代数学・群論の出発点の確立
• 数学に「構造を見る視点」を導入
• 抽象代数学への決定的転換点を形成

これらは、彼の死後に理解され、20世紀数学の発展を根底から支えることになります。

しかし、生前のガロアはほとんど理解されず、論文は拒否され、政治的にも孤立していました。
評価されぬまま時代に押し潰されていった彼の人生は、才能が必ずしも即座に報われるわけではないことを強烈に物語っています。

■ エヴァリスト・ガロアの面白い天才エピソード

● 論文が難解すぎて落とされる
提出した論文は、あまりに先進的すぎて審査員に理解されず、不備扱いされました。
実際には、時代が追いついていなかっただけでした。

● 決闘前夜に理論を書き残す
決闘で死ぬことを悟り、一晩で自身の数学理論を書き残しました。
「時間がない」という言葉が何度も登場する、数学史でも異例の文書です。

● 死後に世界が追いつく
彼の理論は、数十年後にようやく正しく理解され、数学の中心理論となりました。
まさに“未来に生きた数学者”と言える存在です。

📖関連書籍

12. ゲオルク・カントール（1845–1918）

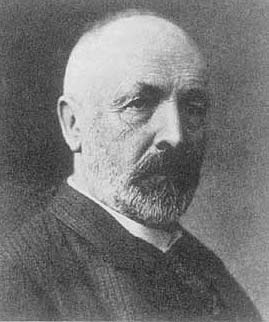
ゲオルク・カントールは、19世紀末から20世紀初頭にかけて活躍したドイツの数学者であり、「無限」を数学の正当な対象として扱えるようにした革命的存在です。

1845年にロシア帝国（現在のサンクトペテルブルク）で生まれ、後にドイツで研究生活を送りました。

カントールの本質は、従来あいまいで哲学的に扱われてきた無限を、厳密な数学的対象として定義し、比較し、分類した点にあります。

彼は「集合」という概念を基盤に、無限にも大小があることを示し、数学の思考領域を根本から拡張しました。

ゲオルク・カントールの代表的な功績としては、以下のような点が挙げられます。

• 集合論の創始による数学基礎の再構築
• 可算無限・非可算無限の区別の導入
• 連続体仮説の提唱
• 数学における無限概念の厳密化

これらの成果は、現代数学のほぼすべての分野の前提条件となっています。

一方で、カントールの思想は当時あまりに革新的すぎたため、強い反発にも遭いました。特にクロネッカーからの激しい批判は、彼の精神に深刻な影響を与えたとされています。

それでもカントールは、「無限は神の与えた理念である」と信じ、研究を手放しませんでした。

■ ゲオルク・カントールの面白い天才エピソード

● 無限にも大小があると証明
「無限はすべて同じ大きさ」という直感を否定し、自然数より実数の方が“多い”ことを示しました。
この発想は、当時の数学者に衝撃を与えます。

● 批判されても引かない
強烈な反対に遭いながらも、自説を撤回することはありませんでした。
後世になって、彼の正しさが全面的に認められています。

● 天才と孤独の象徴
精神的に不安定な時期も多く、評価されぬまま苦しみ続けました。
しかし、その孤独な闘いが数学の地平を押し広げました。

📖関連書籍

13. ジョン・フォン・ノイマン（1903–1957）

ジョン・フォン・ノイマンは、20世紀における最も万能に近い天才数学者であり、数学・物理学・計算機科学・経済学など、驚異的な広がりを持つ分野で決定的な足跡を残した人物です。
1903年にハンガリーで生まれ、後にアメリカへ渡り、科学史に名を刻みました。

フォン・ノイマンの本質は、深い抽象理論と現実的応用を自在に往復できた点にあります。
純粋数学で培った構造理解を、物理学や工学、さらには社会科学へと大胆に接続し、「数学を使って世界を設計する」という姿勢を体現しました。

ジョン・フォン・ノイマンの代表的な功績としては、以下が挙げられます。

• 現代計算機の基本構造（ノイマン型アーキテクチャ）の提唱
• ゲーム理論の基礎確立（ミニマックス定理）
• 関数解析・量子力学の数学的定式化
• セル・オートマトンなど自己複雑系の先駆的研究

これらは、現代社会のテクノロジーや意思決定理論の基盤となっています。

フォン・ノイマンは、抽象数学者でありながら、極めて現実主義的でもありました。
核開発や軍事研究にも関与し、数学の力が持つ光と影の両面を体現した人物とも言えます。

■ ジョン・フォン・ノイマンの面白い天才エピソード

● 人間コンピュータ
コンピュータが普及する以前から、複雑な計算を暗算でこなしていました。
速度と正確さは、周囲が言葉を失うレベルだったと伝えられています。

● 分野横断が当たり前
数学の議論をしていたかと思えば、量子物理、経済理論、戦略論へ自然に移行しました。
「一人で研究所が成立する」と評された天才です。

● 未来を見すぎた男
自己増殖機械や人工知能の可能性を早期に論じていました。
現代になって、彼の発想が次々と現実化しています。

📖関連書籍

14. 劉徽（３世紀頃）

画像出典：Huangdan2060 – Yükleyenin kendi çalışması, CC0, https://commons.wikimedia.org/w/index.php?curid=35060562

劉徽は、3世紀の中国・三国時代に活躍した数学者であり、東洋数学史における最高峰の理論家の一人とされています。

生没年は正確には分かっていませんが、魏の時代に活動し、当時の数学書『九章算術』に詳細な注釈を加えたことで知られています。

劉徽の本質は、計算結果を示すだけでなく、「なぜそうなるのか」を徹底的に論理で説明しようとした点にあります。

それまでの中国数学は実用重視で、証明という概念が弱かったのですが、劉徽は幾何学的直観と論理を用い、数学を理論的学問へと引き上げました。

劉徽の代表的な功績としては、以下のような点が挙げられます。

• 『九章算術』への詳細な注釈と理論的補強
• 円周率の高精度計算（多角形近似法）
• 極限的思考に近い「割円術」の使用
• 体積・面積計算における厳密な論証

これらは、西洋でアルキメデスが行った仕事と非常に近い水準にあり、独立に高度な数学的思考へ到達していたことを示しています。

劉徽は、派手な理論や抽象概念を好んだわけではありません。
あくまで「理解できる数学」「納得できる説明」を重視し、その姿勢は後の中国数学に長く影響を与えました。
東洋における“証明の精神”の源流といえる存在です。

■ 劉徽の面白い天才エピソード

● 証明がないと落ち着かない
答えが合っていても、理由が説明できなければ満足しませんでした。
実用書だった『九章算術』を、理論書に変えてしまった人物です。

● 円を細かく刻み続ける
円を多角形に分割し続けることで円周率を求めました。
考え方は、ほぼ極限概念そのものです。

● 東洋版アルキメデス
後世の研究者からは、「中国のアルキメデス」と評されています。
文化圏を超えて、同じ思考に到達していた例です。

15. シュリニヴァサ・ラマヌジャン（1887–1920）

著者不明Unknown author, CC BY 4.0 https://creativecommons.org/licenses/by/4.0, via Wikimedia Commons

シュリニヴァーサ・ラマヌジャンは、20世紀初頭に現れた最も神秘的で直観的な天才数学者の一人です。
1887年にインドで生まれ、正規の数学教育をほとんど受けないまま、驚異的な数式を次々と生み出しました。

ラマヌジャンの本質は、論理的積み上げよりも、ひらめきと直観によって数式が「見えてしまう」点にあります。

彼のノートには証明のない公式が大量に並んでいましたが、その多くが後に正しいと確認されています。

ラマヌジャンの代表的な功績としては、以下が挙げられます。

• 整数論・分割数理論への決定的貢献
• 無限級数・連分数に関する多数の公式
• モジュラー形式の先駆的発見
• 現代数学にも影響を与えるラマヌジャン予想

これらは、現在でも研究が続くテーマであり、彼の発想が時代を大きく先取りしていたことを示しています。

ラマヌジャンは、イギリスの数学者ハーディとの出会いによって世界的に知られるようになります。

ハーディは「ラマヌジャンは生まれつきの天才」と評し、「彼の公式は、証明できるかどうかよりも、まず正しいかどうかを疑うレベルだった」と語っています。

■ シュリニヴァーサ・ラマヌジャンの面白い天才エピソード

● 数式は神から来る
ラマヌジャンは、自分の数式は女神ナマギリから授けられたと信じていました。
夢の中で公式を受け取ったと語っています。

● 証明はいらない
「正しいと分かるから書いた」という姿勢で難解な数学の公式でノートを埋め尽くしました。
後世の数学者が必死に証明を与えています。

● タクシー数1729
病床のラマヌジャンを訪ねたハーディが「前を走っていたタクシーのナンバーが1729だった。実につまらない数だ」と言うと、
「いいえ、1729は二通りに立方数の和で表せる最小の数です」
と即答しました。自身も優れた数学者であったハーディでさえもその事に瞬時に気づくことは不可能でした。

📖関連書籍

まとめ

いかがだったでしょうか。

この記事では、世界の優れた数学者を１５人ご紹介しました。

ここまでお読みいただきありがとうございました。